The variables that are used to pass values to a subroutine are normally left unchanged. However, actual arguments can also be passed by reference to a subroutine. When an argument is passed by reference, the reference to the variable itself is passed instead of the variable's value. This means that any changes to the variable inside the subroutine are reflected in the variable's value after the subroutine completes. This permits an additional way to return values from a subroutine. To pass a variable by reference we use the var directive in the arguments list. For instance, consider the following program that is meant to swap the values in two integers:
{$APPTYPE CONSOLE}
program Workspace;
procedure Swap(I1,I2 : Integer);
var
Buf : Integer;
begin
Buf := I1;
I1 := I2;
I2 := Buf;
end;
var
X,Y : Integer;
begin
X := 5; Y := 10;
Swap(X,Y);
Writeln('X = ',X,' and ','Y = ',Y);
Readln;
end.
program Workspace;
procedure Swap(I1,I2 : Integer);
var
Buf : Integer;
begin
Buf := I1;
I1 := I2;
I2 := Buf;
end;
var
X,Y : Integer;
begin
X := 5; Y := 10;
Swap(X,Y);
Writeln('X = ',X,' and ','Y = ',Y);
Readln;
end.
This code does not work properly because the actual arguments X and Y are passed by value to Swap which then stores these values for processing in I1 and I2. In other words, X and Y may contain the same values as I1 and I2 initially, but these values are stored in different locations in memory which means that I1 and I2 are discarded after Swap exits. Placing a var directive in the formal argument declaration fixes the problem:
{$APPTYPE CONSOLE}
program Workspace;
procedure Swap(var I1,I2 : Integer);
var
Buf : Integer;
begin
Buf := I1;
I1 := I2;
I2 := Buf;
end;
var
X,Y : Integer;
begin
X := 5; Y := 10;
Swap(X,Y);
Writeln('X = ',X,' and ','Y = ',Y);
Readln;
end.
program Workspace;
procedure Swap(var I1,I2 : Integer);
var
Buf : Integer;
begin
Buf := I1;
I1 := I2;
I2 := Buf;
end;
var
X,Y : Integer;
begin
X := 5; Y := 10;
Swap(X,Y);
Writeln('X = ',X,' and ','Y = ',Y);
Readln;
end.
This code properly swaps the values of X and Y because the actual arguments X and Y are passed by reference to Swap. This means that I1 and I2 reference the same location in memory as X and Y so that any changes to I1 will automatically result in a change in X. Thus, after Swap exits, X contains 10 and Y contains 5.
Subroutines can also have their own local variables which are distinct from the main program's global variables and invisible to the main program and any other subroutines. For instance, consider the following program:
Subroutines can also have their own local variables which are distinct from the main program's global variables and invisible to the main program and any other subroutines. For instance, consider the following program:
{$APPTYPE CONSOLE}
program Workspace;
uses SysUtils;
VAR
Max : Integer = 12;
procedure WriteMulLine(X : Integer);
var
K : Integer;
begin
for K := 1 to Max do Write(Format('%5d,[K*X]));
Writeln;
end;
var
K : Integer;
begin
for K := 1 to Max do
WriteMulLine(K);
Readln;
end.
program Workspace;
uses SysUtils;
VAR
Max : Integer = 12;
procedure WriteMulLine(X : Integer);
var
K : Integer;
begin
for K := 1 to Max do Write(Format('%5d,[K*X]));
Writeln;
end;
var
K : Integer;
begin
for K := 1 to Max do
WriteMulLine(K);
Readln;
end.
This program performs the identical task to one we previously wrote in writing the multiplication tables to the screen. The difference is that we previously used a nested loop with two differently named variables K and J. Here we use K in each loop even though the loops are essentially nested. We can do this because the variable global variable K references a different location in memory than WriteMulLine's local variable K. Also note the use of the global variable Max. Max is used in both loops and references the same location in memory both times. This is because global variables are visible everywhere in the program (as long as they are declared on some line above where they are used) while local variables are visible only within a subroutine. Visibility and a related term scope of variables will be discussed both later in this chapter and later in Unit I.
Excercise 2-18.
Write code to solve the folowing problems.
- Define a procedure that takes 4 arguments: an integer dividend and divisor by value and the whole quotient and remainder by reference. Then call this function and write the quotient and remainder of 10/3 to the screen.
- Define a function called Power that raises any real number Base to a specified integer power Pow and returns the result as a real. Then call this function to write
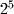 ,
, 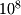 , and
, and 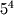 to the screen.
to the screen. - In mathematics, the greek letter sigma
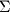 is used to denote a series sum. For example, the following notation concisely represents the sum of integers from 1 to 8:If we replace 8 with
is used to denote a series sum. For example, the following notation concisely represents the sum of integers from 1 to 8:If we replace 8 with
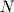 then this notation represents the sum of all integers from 1 to
then this notation represents the sum of all integers from 1 to 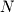 . It can be proven (though we won't do it here) that this sum is given by the following formula:So if
. It can be proven (though we won't do it here) that this sum is given by the following formula:So if
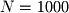 then the sum is
then the sum is 
Verify this formula empirically by first writing an Object Pascal function that loops through all integers from 1 to N and computes their sum and then calling this function with a value of 1000 as the argument.


