Often we encounter situations in which we would like to repeat a command or series of commands. Each repetition is known as an iteration. Sometimes we want to iterate for a fixed number of times and sometimes we do not know when we are designing a program how many iterations are necessary. For this reason, almost all programming languages have at least one loop construct (the exception again being assembler which uses jumps). Object Pascal has 3: for, while, and repeat. A for loop uses a control variable which must be an integer and increments or decrements that variable on each loop iteration. Consider the following program which counts down from 10 and then back up to 10:
{$APPTYPE CONSOLE}
program ForLoop;
var
K : Integer;
begin
For K := 10 downto 0 do Writeln(K);
For K := 1 to 10 do Writeln(K);
Readln;
end.
program ForLoop;
var
K : Integer;
begin
For K := 10 downto 0 do Writeln(K);
For K := 1 to 10 do Writeln(K);
Readln;
end.
If you copy/paste this program into the editor and run it you will see that it writes the numbers between 10 and 0 to the screen and then 0 to 10 on the next line. This could have also been accomplished without a loop, but it would have required a total of 21 Writeln statements.
Break and Continue are also common statements that appear in Object Pascal loops (and in most other languages for that matter). Break exits the loop immediately even if it has not completed. Continue exits the current iteration of the loop and starts the next iteration.
Break and Continue are also common statements that appear in Object Pascal loops (and in most other languages for that matter). Break exits the loop immediately even if it has not completed. Continue exits the current iteration of the loop and starts the next iteration.
Excercise 2-14.
Write code to solve the following problems. Remember if you need to debug any of them you have to use the {$I Debug.inc} line right after begin if you are using Lazarus.
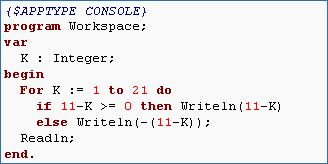
- Write a program that gives output identical to the program above but uses only a single loop instead of two. Hint: You will need to use the absolute value function Abs.
- Write a program that gives output identical to the previous program but do not use the Abs function. Hint: You will need an if statement.
- Write a program that displays the powers of 2 from
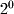 to
to 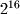 in the following form without using the Power function in Math. 2^0 = 1
in the following form without using the Power function in Math. 2^0 = 1
2^1 = 2
2^2 = 4
...
2^16 = 65536Hint: You will need both the for loop control variable and an additional variable to store each sequential power of 2. - Display the line 'The "X" key is down.' where X is any letter from A to Z. Hint: Start with copying and pasting the code that does this for the A key and rewrite it so that it is a loop. Keep in mind the Chr function converts a number to a character.if Keyboard[Ord('A')].Down then
TextOut(0,0,'The "A" key is down.');Now think of how you could write a loop for this that would loop from A to Z.
Loops can be nested, but nested loops must use different control variables:
{$APPTYPE CONSOLE}
program Workspace;
var
K,J : Integer;
begin
Writeln('The multiplication tables up to 12:');
For K := 1 to 12 do
begin
For J := 1 to 12 do Write(K*J,' ');
Writeln;
end;
Readln;
end.
program Workspace;
var
K,J : Integer;
begin
Writeln('The multiplication tables up to 12:');
For K := 1 to 12 do
begin
For J := 1 to 12 do Write(K*J,' ');
Writeln;
end;
Readln;
end.
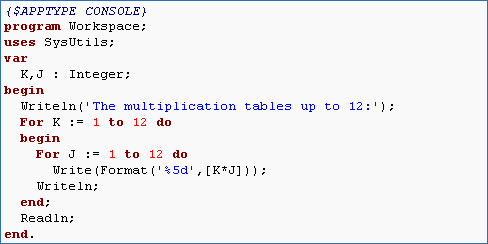
If you run this program you will see that it prints out the multiplication tables up to 12. Note the begin and end under the first for loop. This is necessary because this loop contains two simple statements For J := 1 to 12 do Write(K*J,' '); and Writeln;. Without the begin and end compound statement, Writeln; would not be part of the loop. Try removing the begin and end and see what happens.
Excercise 2-15.
The previous code does not produce a table with aligned columns. This results because not all of the integers have the same number of digits. Using the Format function, make all of the columns have the same width of 5 characters. Hint: Refer to the SysUtils table in Section 2.7.
Excercise 2-16.
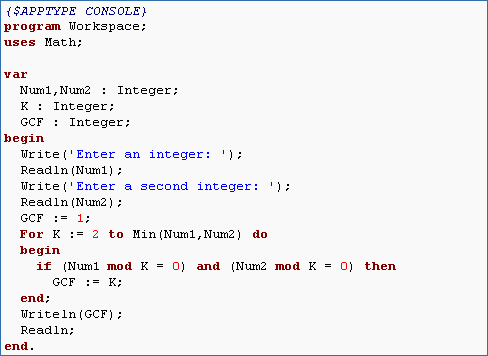
In this exercise we will write a simple program that computes the greatest common factor (GCF) and least common multiple of two numbers.
- Write a boolean expression that would return True if both Num1 and Num2 were evenly divisible by SomeNum (i.e., SomeNum is a common factor to both Num1 and Num2).
- Write a program that reads in two integers (Num1 and Num2) and then loops through using the Boolean expression from the previous problem to write the evenly divisible factors of Num1 and Num2 that are greater than 1 to the screen. Keep in mind that there is no need to list factors greater than the smaller of Num1 or Num2 (i.e., this will determine the upper bound for the for loop). Use {$I Debug.inc} directly after begin if you need to set breakpoints for debugging.
- Now alter this program so that it returns only the greatest common factor. The best way to do this is to assume that there are no common factors (i.e. GCF = 1) and then update GCF when a common factor is discovered.
- As the program is written now, all numbers between 2 and Min(Num1,Num2) have to be tested. Rewrite the loop so that it can exit as soon as the greatest common factor is discovered.
- Now we will write a program to determine the least common multiple. Think carefully about how to do this. If you take the smaller of the two integers and start multiplying 2, 3, 4, etc times this integer, how can you determine if a multiple of the smaller integer is also a multiple of the larger integer? Hint: If K is an integer multiplier, SmallerNum*K is an integer multiple of SmallerNum. How can we determine if SmallerNum*K is a common multiple of LargerNum?
- Use the result of the previous problem to write the program to determine the least common multiple. Keep in mind that you need to loop only far enough to find the first common multiple (because this will be the least common multiple).