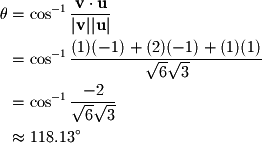Like vector/vector addition and subtraction, the dot product has a geometric interpretation: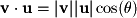 
This formula can be used to determine the angle 
between two vectors as shown in Figure 2-7.
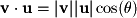
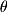between two vectors as shown in Figure 2-7.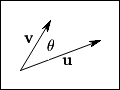 
Figure 2-7.
Geometry of the Dot Product
Say that we want to find the angle between the following vectors: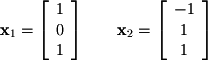
We can first rearrange the definition of the dot product to solve for 
:
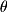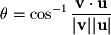The dot product of the two vectors gives the following: 
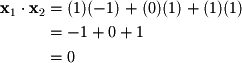Thus we have the following for 
: 
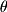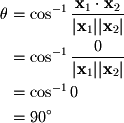In this case, the angle between the two vectors was 
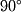. Formally we can write this as 
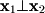which is read "
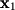is perpendicular to 
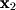". This example actually illustrates an important use of the dot product that appears many times in linear algebra. To test if two vectors are perpendicular, we simply verify that the dot product is equal to 
:
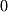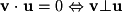
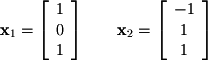
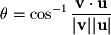
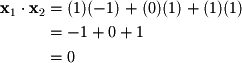
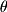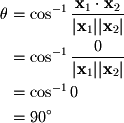
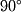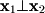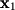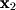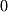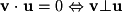
:: . Formally we can write this as which is read " is perpendicular to ". This example actually illustrates an important use of the dot product that appears many times in linear algebra. To test if two vectors are perpendicular, we simply verify that the dot product is equal to :Excercise 2-6.
Find the angle between the following vectors: 
