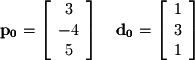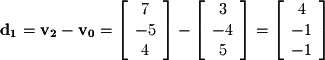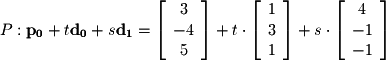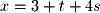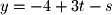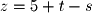The parametric form for a plane can be derived similarly. Three non-colinear points are required to define a plane. Lets take 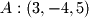 ,
,  , and
, and 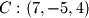 . Once again we take A as the starting point
. Once again we take A as the starting point 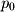 which means we already have one direction vector from before:
which means we already have one direction vector from before: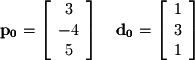 Now we simply need a second direction vector to define a plane:
Now we simply need a second direction vector to define a plane: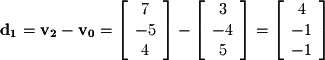 Given these vectors we can write the parametric form of a plane as the following:
Given these vectors we can write the parametric form of a plane as the following: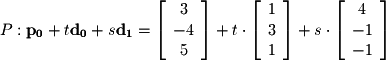 It is also important to note that we have been using the vector parameterization of lines and planes in the above examples. Parametric equations can also be used to define the parametric form of a line or plane. For example, the vector parameterization above is equivalent to the following parametric equations:
It is also important to note that we have been using the vector parameterization of lines and planes in the above examples. Parametric equations can also be used to define the parametric form of a line or plane. For example, the vector parameterization above is equivalent to the following parametric equations: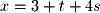
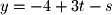
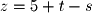
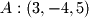 ,
,  , and
, and 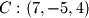 . Once again we take A as the starting point
. Once again we take A as the starting point 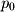 which means we already have one direction vector from before:
which means we already have one direction vector from before: