There are several types of matrices that you should be familiar with. First, a square matrix is any matrix of 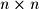 dimensions. For example, the following matrices are square matrices of 2x2 and 3x3 dimensions respectively:
dimensions. For example, the following matrices are square matrices of 2x2 and 3x3 dimensions respectively: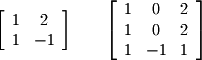 A diagonal matrix is a square matrix with zero or non-zero entries along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 diagonal matrices:
A diagonal matrix is a square matrix with zero or non-zero entries along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 diagonal matrices: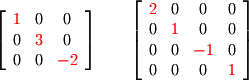 An upper triangular matrix, usually denoted
An upper triangular matrix, usually denoted 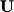 , is a matrix with zero or non-zero entries in and above the diagonal and with zeros elsewhere. The following are examples of a square 3x3 upper triangular matrix and a rectangular 3x5 upper triangular matrix:
, is a matrix with zero or non-zero entries in and above the diagonal and with zeros elsewhere. The following are examples of a square 3x3 upper triangular matrix and a rectangular 3x5 upper triangular matrix: 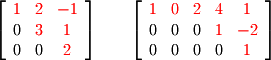 A lower triangular matrix, usually denoted
A lower triangular matrix, usually denoted  , is likewise a matrix with zero or non-zero entries in and below the diagonal and with zeros elsewhere. One can also define strictly upper/lower triangular matrices in which the diagonals are also zeros but these find limited application in introductory coursework.
, is likewise a matrix with zero or non-zero entries in and below the diagonal and with zeros elsewhere. One can also define strictly upper/lower triangular matrices in which the diagonals are also zeros but these find limited application in introductory coursework.
Finally, the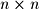 identity matrix
identity matrix  is a diagonal matrix with entries of 1 along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 identity matrices:
is a diagonal matrix with entries of 1 along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 identity matrices:  Now that we have defined the basic mathematical objects of linear algebra, we will discuss the basic operations that can be performed on them in the following chapter.
Now that we have defined the basic mathematical objects of linear algebra, we will discuss the basic operations that can be performed on them in the following chapter.
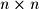 dimensions. For example, the following matrices are square matrices of 2x2 and 3x3 dimensions respectively:
dimensions. For example, the following matrices are square matrices of 2x2 and 3x3 dimensions respectively: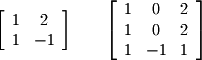

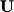 , is a matrix with zero or non-zero entries in and above the diagonal and with zeros elsewhere. The following are examples of a square 3x3 upper triangular matrix and a rectangular 3x5 upper triangular matrix:
, is a matrix with zero or non-zero entries in and above the diagonal and with zeros elsewhere. The following are examples of a square 3x3 upper triangular matrix and a rectangular 3x5 upper triangular matrix: 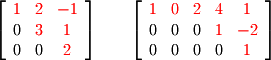
 , is likewise a matrix with zero or non-zero entries in and below the diagonal and with zeros elsewhere. One can also define strictly upper/lower triangular matrices in which the diagonals are also zeros but these find limited application in introductory coursework.
, is likewise a matrix with zero or non-zero entries in and below the diagonal and with zeros elsewhere. One can also define strictly upper/lower triangular matrices in which the diagonals are also zeros but these find limited application in introductory coursework.Finally, the
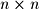 identity matrix
identity matrix 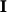 is a diagonal matrix with entries of 1 along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 identity matrices:
is a diagonal matrix with entries of 1 along the diagonal and zeros elsewhere. The following are 3x3 and 4x4 identity matrices: 