Higher dimensional spaces (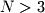
) are more difficult to visualize. While 2D and 3D spaces seem readily applicable to every day life, higher dimensional spaces seem far more abstract. In order for you to enter linear algebra with a better understanding of N-dimensional space, let's start with a basic example. Consider a textbook. In 3D space we describe the textbook with width, height, and depth. These three variables are geometric properties of the textbook. We will find that geometry is one of the many important applications of linear algebra. For instance, operations in linear algebra (such as rotations, translations, and projections) are at the heart of modern computer graphics and thus all engineering design packages and 3D computer games.
However, not all variables need to have a geometric meaning. We can make the description of the textbook richer by adding additional variables such as color, copyright year, author name, and page count. Since we have added 4 more variables to the description, we call this a 7-dimensional space (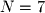
). It is important for you to realize that although this text makes use of geometry in order to build a more intuitive understanding of concepts, linear algebra can be used to deal with any type of variable.
What often occurs in applications of linear algebra is that variables are given a geometric meaning in order to help visualize their relationships to one another. Consider an application of linear algebra to science in which an experiment is conducted on a balloon filled with air. The temperature of the gas inside the balloon is varied while the pressure is held constant. We already know from every day life that as the temperature increases the balloon should expand. Figure 1-4 shows a 2-dimensional plot of the volume of the balloon at several different temperatures. Notice that the points almost all fall along a line. Thus, we can say there is a linear relationship between temperature and volume--a fact which is known in science as Charles's Law.
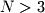) are more difficult to visualize. While 2D and 3D spaces seem readily applicable to every day life, higher dimensional spaces seem far more abstract. In order for you to enter linear algebra with a better understanding of N-dimensional space, let's start with a basic example. Consider a textbook. In 3D space we describe the textbook with width, height, and depth. These three variables are geometric properties of the textbook. We will find that geometry is one of the many important applications of linear algebra. For instance, operations in linear algebra (such as rotations, translations, and projections) are at the heart of modern computer graphics and thus all engineering design packages and 3D computer games.However, not all variables need to have a geometric meaning. We can make the description of the textbook richer by adding additional variables such as color, copyright year, author name, and page count. Since we have added 4 more variables to the description, we call this a 7-dimensional space (
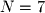). It is important for you to realize that although this text makes use of geometry in order to build a more intuitive understanding of concepts, linear algebra can be used to deal with any type of variable. What often occurs in applications of linear algebra is that variables are given a geometric meaning in order to help visualize their relationships to one another. Consider an application of linear algebra to science in which an experiment is conducted on a balloon filled with air. The temperature of the gas inside the balloon is varied while the pressure is held constant. We already know from every day life that as the temperature increases the balloon should expand. Figure 1-4 shows a 2-dimensional plot of the volume of the balloon at several different temperatures. Notice that the points almost all fall along a line. Thus, we can say there is a linear relationship between temperature and volume--a fact which is known in science as Charles's Law.
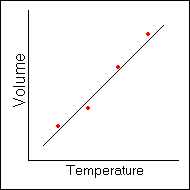
Figure 1-4.
Charles's Law Experiment
But what if we want to know the equation of a line that passes through these points. Since these points do not lie on the same line we cannot apply the techniques from elementary algebra to determine the proper linear equation. Linear algebra provides techniques that allow us to determine the line that is closest to all the given points. This line is known as the "best-fit" line to the data set. More complicated experiments with many more than 2 variables are common in science and engineering and the concepts behind N-dimensional space allow us to deal with such situations.
Before we move on, there are a few things you should keep in mind when using this book. You should be advised not to skip around. If you do not understand a concept, work on it before moving on. Care was taken when writing this book not to waste words, so read all of them carefully (and maybe even two or three times). The great difficulty for most students in linear algebra and in college-level coursework in general is the failure to develop a proper conceptual framework for the material. This book attempts to build such a framework, but one must pay attention and follow its lead rather than haphazardly fumbling through it. So take it slow and make sure you have given yourself enough time to read through it (i.e., do not wait until the night before the exam). With that said, turn the page (if you are reading in print) or click to the next subsection.
Before we move on, there are a few things you should keep in mind when using this book. You should be advised not to skip around. If you do not understand a concept, work on it before moving on. Care was taken when writing this book not to waste words, so read all of them carefully (and maybe even two or three times). The great difficulty for most students in linear algebra and in college-level coursework in general is the failure to develop a proper conceptual framework for the material. This book attempts to build such a framework, but one must pay attention and follow its lead rather than haphazardly fumbling through it. So take it slow and make sure you have given yourself enough time to read through it (i.e., do not wait until the night before the exam). With that said, turn the page (if you are reading in print) or click to the next subsection.