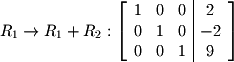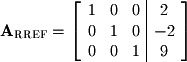In order to find the REF and RREF forms of a matrix, both Gaussian and Gauss-Jordan Elimination use a process called row reduction which involves three elementary row operations:
- Interchanging two rows (
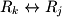). - Adding a multiple of one row to another (
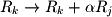). - Multiplying any row by a nonzero scalar value (
).
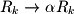The notation shown here is somewhat common, but again, different texts adopt different conventions so check your own to make sure. By selecting and applying these operations iteratively, one can take any matrix first to REF and then to RREF. You should realize that row reduction is an iterative algorithm. That means that there is a very systematic approach to performing it which is both good and bad. The good part is that once you learn it, it is not difficult to apply. The bad part is that it is very tedious to apply (especially for large matrices) and lends itself to plenty of opportunities for careless mistakes in arithmetic. For this reason it is strongly advised that you double check each step (watch especially for sign errors).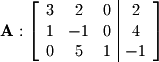
We always start by inspecting the first non-zero column from the left to right. Start by moving any row which has a 1 in it to the top of the matrix. Any row with a 0 should be moved to the bottom. If there are no ones, apply row op #3 in order to multiply by a value that will yield a 1. For our matrix, the second row needs to be moved to the top: 
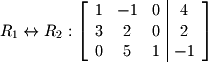Next, perform any operations necessary to obtain 
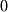's below the pivot in that column: 
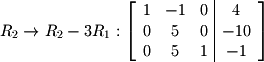Move to the next column and find the pivot (in this case 
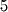). Now, again, apply any operations to obtain 
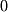's below the pivot (don't worry about the entries above pivots yet). 
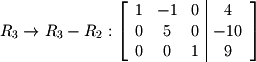Multiply the second row by 1/5 in order to obtain a 1 in the pivot position. 
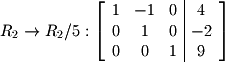At this point the matrix is in REF. We could stop here and conver the matrix back to equation form: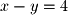 
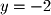
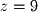By substituting the value of 
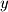into the first equation we can find that 
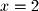. This method of solving a system is known as Gaussian Elimination with Back Substitution. Back Substitution is often the quickest way of solving a system.
The matrix could have also been taken all the way to RREF. In the case of this matrix, we are lucky and the third column has zero's above the pivot. If this were not the case we would start by moving backwards from right to left across the columns in order to get the needed zeros. For now we need only one more operation: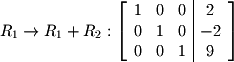
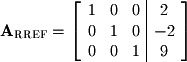Taking the system all the way to RREF to obtain the solution is known as Gauss-Jordan Elimination.
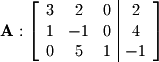
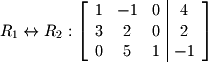
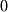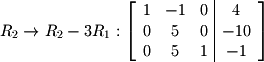
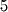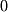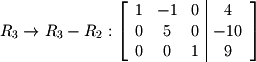
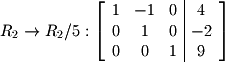
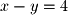
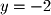
's below the pivot in that column: ). Now, again, apply any operations to obtain 's below the pivot (don't worry about the entries above pivots yet). into the first equation we can find that 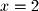. This method of solving a system is known as Gaussian Elimination with Back Substitution. Back Substitution is often the quickest way of solving a system.The matrix could have also been taken all the way to RREF. In the case of this matrix, we are lucky and the third column has zero's above the pivot. If this were not the case we would start by moving backwards from right to left across the columns in order to get the needed zeros. For now we need only one more operation: