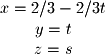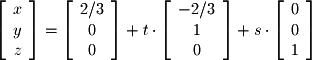We now know that systems can have either no solution, a unique solution, or an infinite solution. Moreover, the infinite solution has a specific dimension dependening on how the system is constrained by independent equations. The nature of the solution of systems used previously has been somewhat obvious due to the limited number of variables and equations used. In real-life practice, many hundreds of equations and variables may be needed to specify a system. As they have done before, matrix operations allow a very systematic approach to be applied to determine the nature of a system's solution.
Let's start with the system with a unique solution. Gauss-Jordan Elimination can be applied to obtain the following: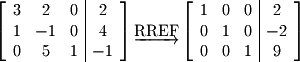
A system has a unique solution if there is a pivot in every column. This type of matrix is said to have a rank of 3 where rank is equal to the number of pivots. Since the rank is equal to the number of columns, the matrix is called a full-rank matrix.
Next we have the system with no solutions. Gauss-Jordan Elimination can be applied to obtain the following: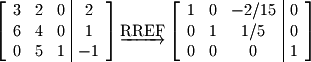
Note that the last row of the RREF matrix does not hold a pivot but a "1" appears in the constant vector on the right hand side of the matrix. If one converts this row of the matrix back to equation form, the result is 
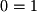which does not make any sense. Therefore, a system has no solution if a constant appears in a row that has no pivot.
Now we'll move to the system with infinite solutions along one dimension: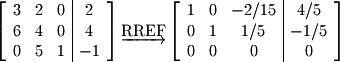
The last row of the RREF matrix does not have a pivot just like the last matrix but the entry in the constant matrix is 
which yields 
or a proper result. This matrix is said to have a rank of 2 and a 1 dimensional solution (# columns - rank = # solutions). How can we specify this solution since it is infinite along one dimension? We turn to the parametric form of a line. First, convert the RREF matrix back to equation form: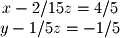
One of the variables needs to be redefined as the free variable. It does not matter which one you choose, but it is common to choose the variable whose column does not contain a pivot. So in this case we set 
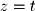and solve for 
and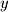 
:
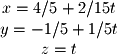Now we have the parametric equations that represent the solution of the system in 
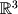. We can also write the vector parameterization as we have learned before: 
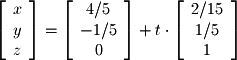Finally, we will deal with the system with a 2-dimensional infinite solution: 
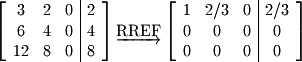This system has a rank of 1 since it has only one pivotal column. Once again we convert to equation form: 
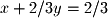We need 2 free variables so we will set 
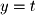and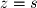 
. 
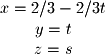
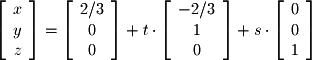
Let's start with the system with a unique solution. Gauss-Jordan Elimination can be applied to obtain the following:
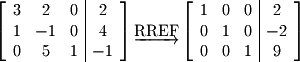
Next we have the system with no solutions. Gauss-Jordan Elimination can be applied to obtain the following:
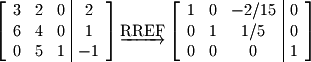
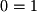which does not make any sense. Therefore, a system has no solution if a constant appears in a row that has no pivot.Now we'll move to the system with infinite solutions along one dimension:
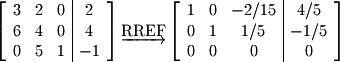
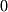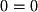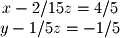
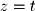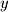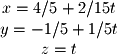
which yields or a proper result. This matrix is said to have a rank of 2 and a 1 dimensional solution (# columns - rank = # solutions). How can we specify this solution since it is infinite along one dimension? We turn to the parametric form of a line. First, convert the RREF matrix back to equation form: and solve for and :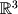. 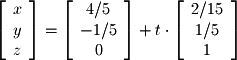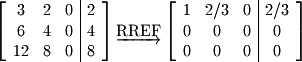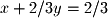We can also write the vector parameterization as we have learned before: 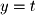and 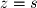.