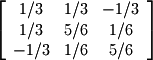An orthogonal projection onto a subspace is defined as  where
where  is a matrix made up of the vectors that form a basis for the subspace. Think of an othogonal projection like this... it is the linear transformation that projects a "shadow" of a vector onto a subspace as if a light were held exactly at
is a matrix made up of the vectors that form a basis for the subspace. Think of an othogonal projection like this... it is the linear transformation that projects a "shadow" of a vector onto a subspace as if a light were held exactly at  to the subspace and above the vector.
to the subspace and above the vector.
 where
where  is a matrix made up of the vectors that form a basis for the subspace. Think of an othogonal projection like this... it is the linear transformation that projects a "shadow" of a vector onto a subspace as if a light were held exactly at
is a matrix made up of the vectors that form a basis for the subspace. Think of an othogonal projection like this... it is the linear transformation that projects a "shadow" of a vector onto a subspace as if a light were held exactly at  to the subspace and above the vector.
to the subspace and above the vector. Excercise 7-4.
Find the orthogonal projection onto the plane 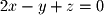 in
in 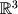 .
.
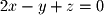 in
in 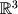 .
. 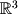 and we have 1 equation, we know that two of the variables must be free parameters. Thus if we set
and we have 1 equation, we know that two of the variables must be free parameters. Thus if we set 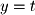 and
and 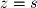 we can find the basis for the plane:
we can find the basis for the plane: 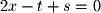
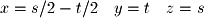
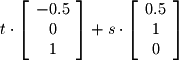 .
.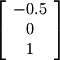 and
and 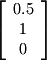 are free vectors and thus form the basis.
are free vectors and thus form the basis.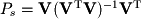 where
where  Doing the appropriate calculations yields the following for
Doing the appropriate calculations yields the following for 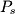 :
: