As an example, let's use the matrix from the previous subsection: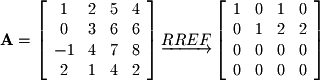 From this row reduction we can see that the column space (image) has the following basis:
From this row reduction we can see that the column space (image) has the following basis: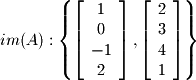 The pivotal columns of matrix
The pivotal columns of matrix 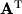 are the pivotal rows of
are the pivotal rows of 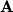 so the rows with pivots in the original matrix form the basis of the row space (coimage):
so the rows with pivots in the original matrix form the basis of the row space (coimage):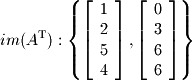 For the null space (kernel), we solve the system
For the null space (kernel), we solve the system 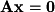 . This is, of course, equivalent to simply row reducing
. This is, of course, equivalent to simply row reducing 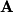 since the constant vector is
since the constant vector is 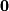 . First convert the matrix above back into equation form:
. First convert the matrix above back into equation form: 
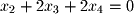 Next, we set
Next, we set 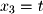 and
and 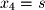 and parameterize the solution as follows:
and parameterize the solution as follows: 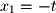

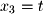
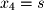
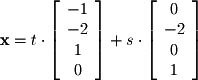 Thus, we can write the basis for the null space (kernel) as the following:
Thus, we can write the basis for the null space (kernel) as the following: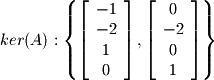 We will not show the basis for the left nullspace as it is rarely used in practice, but it can be found by applying the same method for finding the null space to
We will not show the basis for the left nullspace as it is rarely used in practice, but it can be found by applying the same method for finding the null space to 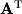 .
.
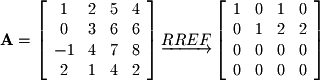

 are the pivotal rows of
are the pivotal rows of 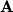 so the rows with pivots in the original matrix form the basis of the row space (coimage):
so the rows with pivots in the original matrix form the basis of the row space (coimage):
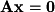 . This is, of course, equivalent to simply row reducing
. This is, of course, equivalent to simply row reducing 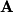 since the constant vector is
since the constant vector is 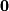 . First convert the matrix above back into equation form:
. First convert the matrix above back into equation form: 
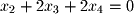
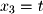 and
and 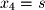 and parameterize the solution as follows:
and parameterize the solution as follows: 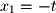

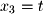
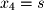
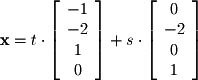
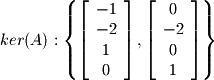
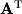 .
.