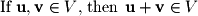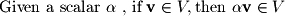The span of a set of vectors is simply another set of vectors, but it is an infinite set of vectors. An infinite set of vectors is known as a vector space. Any 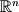 is a vector space, and many of the objects in
is a vector space, and many of the objects in 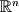 such as lines through the origin and planes through the origin are also vector spaces. The key phrase is "through the origin." Notice that this is necessary based on the definitoin of a span. If all the free parameters are set to 0 then the zero vector is obtained.
such as lines through the origin and planes through the origin are also vector spaces. The key phrase is "through the origin." Notice that this is necessary based on the definitoin of a span. If all the free parameters are set to 0 then the zero vector is obtained.
A vector space within a vector space is called a subspace. We say that is a subspace of
is a subspace of 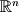 . Likewise, a plane through the origin in
. Likewise, a plane through the origin in  is a subspace of
is a subspace of  .
.
Formally, a vector space is defined by the following: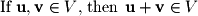
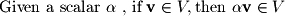 In words, we say this definition states that vector spaces are closed under addition and scalar multiplication. This means that if we choose any two vectors in the space and multiply them by any constant and add them together, the result should be a vector that also lies in this space.
In words, we say this definition states that vector spaces are closed under addition and scalar multiplication. This means that if we choose any two vectors in the space and multiply them by any constant and add them together, the result should be a vector that also lies in this space.
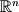 is a vector space, and many of the objects in
is a vector space, and many of the objects in 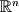 such as lines through the origin and planes through the origin are also vector spaces. The key phrase is "through the origin." Notice that this is necessary based on the definitoin of a span. If all the free parameters are set to 0 then the zero vector is obtained.
such as lines through the origin and planes through the origin are also vector spaces. The key phrase is "through the origin." Notice that this is necessary based on the definitoin of a span. If all the free parameters are set to 0 then the zero vector is obtained.A vector space within a vector space is called a subspace. We say that
 is a subspace of
is a subspace of 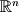 . Likewise, a plane through the origin in
. Likewise, a plane through the origin in  is a subspace of
is a subspace of  .
.Formally, a vector space is defined by the following: