Example 3-11 illustrates a number of very important points concerning algorithms. First, there are often many ways to write an algorithm to solve a particular problem. Each way is generally either more or less efficient than some other way. Finding the most efficient solution often requires careful consideration of the properties of the problem that may not be immediately obvious given the definition of the problem. What exactly do we mean by this? The definition of a greatest common factor is the greatest number that evenly divides both numbers. From this definition, we created SlowGCF which simply started at the smaller number and looped backwards checking for even divisibility until a valid common factor was found. We could have looped forward of course from 2 until the smaller number but this would have required testing all numbers up to the smaller number since we are looking for the greatest common factor. Looping backwards was a first small step in improving efficiency. This type of algorithm is often called a brute force approach.
A brute force algorithm is one that considers all the possible solutions and tests each one. Brute force can be useful for simple problems such as finding the gcf of small numbers like 40 and 16. For instance, consider the situation in which you needed quick factorization of small numbers and had no prior knowledge of Euclid's algorithm. The fastest way for you to solve the problem is to use the brute force approach that is SlowGCF. Even though we branded it as "slow" you will notice that it still takes only milliseconds to run. However, if we need to run this algorithm hundreds or thousands of times, we need to optimize it. Fortunately, for a great many problems in computer science and mathematics there exist well-known efficient algorithms to solve these problems (for example, sorting an array or searching for an item in a list). As the saying goes, days of coding can save you a 15 minute online search for a known algorithm.
Another facet of efficiency is its dependence on the inputs to the algorithm. Running SlowGCF on 40 and 16 a thousand times results in 9000 iterations. Running SlowGCF on 8704 and 22016 results in over 8 million iterations. The rate limiting step of SlowGCF is the smaller of the two numbers. For example, 10 and 22016 requires only 9 iterations because we check all numbers between 2 and 10 inclusive. In the worst case, we would have to iterate N times where N is the number of iterations. For example, with 22016 and 8707 we have to iterate 8707 times because the only common factor is 1 (8707 is prime). The worst case is usually given as a quantitative measure of the algorithms efficiency. In a later unit we will describe this in detail with what is known as big-O notation. You do not have to worry about this now but we introduce it for future reference. Big-O notation describes the growth rate of an algorithm with respect to its inputs. In other words, how many steps are required to solve the problem given the size of the inputs. SlowGCF is O(N) where N is the size of the smaller input. This means that its worst case grows linearly with N. It is said to have linear computational complexity. In practice, this isn't so bad. Many problems have exponential computational complexity or O(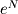
) which makes them impractical on modern processors. Although we will not explain why here, FastGCF never requires more iterations than 5 times the number of digits in the smaller number (Assuming that the smaller number is given in B. If not, it requires 1 additional iteration to swap the two). As a side note, this was proven mathematically in the 1800s and marked the beginning of computational complexity theory. This means that without knowing anything else, we can safely say that finding the gcf of 8704 and 22016 with FastGCF takes no more than 5*(4 digits in 8704) = 20 iterations. We know from running it that it actually takes 5 iterations. Remember that when we define complexity we are talking only about the very worst case and not what actually happens most of the time or even on average. For example, let's put FastGCF into a bad case (but not necessarily the worst case) with 8707 and 22016. Here it actually takes 12 iterations to find that the gcf is 1 since 8707 is prime which is less than 20 iterations predicted for the worst case. Now let's try 144 and 89. 89 has two digits so the worst case is 2*5 = 10 iterations. When we run FastGCF(144,89) we see that it does indeed take exactly 10 iterations so 144 and 89 is an example of the worst case scenario for FastGCF. Still, this is extremely fast compared to SlowGCF which also has a worst case with 144 and 89 and requires 89 iterations.
Can we write this statement about FastGCF's number of iterations as a mathematical formula? Since base 10 logs are proportional to the number of digits in a number (e.g. log(10) = 1, log(100) = 2, log(1000) = 3), we can define the number of digits as floor(log(N)+1) where N is the smaller number and floor truncates the decimal part (e.g., floor(10.3) = 10 and floor(10.8) = 10). Using this definition, the maximum number of iterations is 5*floor(log(N)+1). Now we can write this in big-O notation as O(5*floor(log(N)+1)). In big-O notation, we only care about the rate with respect to N. For example,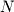
and 
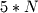are both linear and 
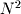and 
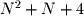are both quadratic. Because of this, O(N) and O(5*N) are considered equivalent (they both have linear complexity). With respect to FastGCF, O(5*floor(log(N)+1)) and O(log(N)) are equivalent because they both have logarithmic complexity. So, we succinctly write that the complexity of FastGCF is O(log(N)). Again, do not worry about the details of big-O notation here. It is completely unimportant to the basic programming presented in this unit. It will become extremely important in future units though when we try to compare algorithms. To develop a very basic understanding of what this means, remember that exponentials and factorials are some of the fastest growing functions and logarithms are some of the slowest growing functions in mathematics.
While we discuss the importance of algorithmic efficiency at length, we should also point out that a common pitfall of novice programmers (and even experienced programmers accidentally) is to over-optimize a program. Ultimately, the fastest program is one written entirely in low-level assembly with care taken to optimize each section of code by hand. In practice, this would take eons and is simply absurd. High-level languages like Object Pascal and C++ already do their best at automatically optimizing code when they translate to assembly during compile. Of course, they cannot convert SlowGCF to FastGCF because they have no in depth knowledge about the nature of the problem of finding the greatest common factor as humans do. But as we pointed out earlier, if the purpose of the program is to compute gcfs only for small numbers or to compute a gcf only once, SlowGCF does the job just fine. If however, we are writing a mathematics library that will be used by lots of other programs, we would want to use FastGCF. The lesson here is that you should always get your code working first before worrying about optimizations. Once you know it works, then you can look for bottlenecks or parts of the code that significantly slow down the rest of the program. Loops are almost always the location of bottlenecks. But some loops are called so infrequently in a program that there is no reason to optimize them. Adopting the "good-enough" solution can save hours of programming. Parts of code that are called very frequently are called performance critical parts of code and should be optimized, but only after the program is finished. There is no reason to optimize something that does not work in the first place.
Having the fewest number of iterations is often but not always a sign of the best algorithm. If what goes on inside an iteration is very computationally complex, another algorithm with more iterations but simpler computations may be better. Again this depends on the kind of inputs you intend to feed the algorithm. This is also one of the reasons we write big-O notation as O(N) even if the actual worst case is 4*N+1 or O(log(N)) if the worst case is 5*floor(log(N)+1). We do not care about being exact in terms of the number of iterations because if one algorithm has a worst case of N and another has 4*N+1 what really matters is what happens inside the iteration and not the number of iterations. On the other hand, if one algorithm is 4*N+1 and another is 5*floor(log(N)+1), you should almost always choose the latter. To understand why, consider what happens if N = 10000. For the first one, the worst-case is 4*10000+1 = 40001. For the second, the worst case is 5*floor(log(10000)+1) = 25. It does not really matter what happens inside the iteration if one is repeated 40,001 times and the other only 25 times. Defintely pick the 25. Thus, as a general rule, algorithms that belong to the same complexity class (such as O(log N)) are pretty much equivalent unless one uses simpler operations inside the iteration. In general, the best algorithms are O(1) constant complexity, O(log N) logarithmic complexity, O(N) linear complexity, O(N^a) polynomial complexity, and O(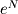
) exponential complexity. Keep in mind that this is only a very small sampling of algorithm complexity. Complexity analysis is a very rich field that is well beyond the scope of this book (even the later units). Given that you have two algorithms in the same complexity class, the best one of the two will be the one that minimizes the use of floating point division (one of the most expensive operations) or large memory allocations.
A brute force algorithm is one that considers all the possible solutions and tests each one. Brute force can be useful for simple problems such as finding the gcf of small numbers like 40 and 16. For instance, consider the situation in which you needed quick factorization of small numbers and had no prior knowledge of Euclid's algorithm. The fastest way for you to solve the problem is to use the brute force approach that is SlowGCF. Even though we branded it as "slow" you will notice that it still takes only milliseconds to run. However, if we need to run this algorithm hundreds or thousands of times, we need to optimize it. Fortunately, for a great many problems in computer science and mathematics there exist well-known efficient algorithms to solve these problems (for example, sorting an array or searching for an item in a list). As the saying goes, days of coding can save you a 15 minute online search for a known algorithm.
Another facet of efficiency is its dependence on the inputs to the algorithm. Running SlowGCF on 40 and 16 a thousand times results in 9000 iterations. Running SlowGCF on 8704 and 22016 results in over 8 million iterations. The rate limiting step of SlowGCF is the smaller of the two numbers. For example, 10 and 22016 requires only 9 iterations because we check all numbers between 2 and 10 inclusive. In the worst case, we would have to iterate N times where N is the number of iterations. For example, with 22016 and 8707 we have to iterate 8707 times because the only common factor is 1 (8707 is prime). The worst case is usually given as a quantitative measure of the algorithms efficiency. In a later unit we will describe this in detail with what is known as big-O notation. You do not have to worry about this now but we introduce it for future reference. Big-O notation describes the growth rate of an algorithm with respect to its inputs. In other words, how many steps are required to solve the problem given the size of the inputs. SlowGCF is O(N) where N is the size of the smaller input. This means that its worst case grows linearly with N. It is said to have linear computational complexity. In practice, this isn't so bad. Many problems have exponential computational complexity or O(
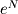) which makes them impractical on modern processors. Although we will not explain why here, FastGCF never requires more iterations than 5 times the number of digits in the smaller number (Assuming that the smaller number is given in B. If not, it requires 1 additional iteration to swap the two). As a side note, this was proven mathematically in the 1800s and marked the beginning of computational complexity theory. This means that without knowing anything else, we can safely say that finding the gcf of 8704 and 22016 with FastGCF takes no more than 5*(4 digits in 8704) = 20 iterations. We know from running it that it actually takes 5 iterations. Remember that when we define complexity we are talking only about the very worst case and not what actually happens most of the time or even on average. For example, let's put FastGCF into a bad case (but not necessarily the worst case) with 8707 and 22016. Here it actually takes 12 iterations to find that the gcf is 1 since 8707 is prime which is less than 20 iterations predicted for the worst case. Now let's try 144 and 89. 89 has two digits so the worst case is 2*5 = 10 iterations. When we run FastGCF(144,89) we see that it does indeed take exactly 10 iterations so 144 and 89 is an example of the worst case scenario for FastGCF. Still, this is extremely fast compared to SlowGCF which also has a worst case with 144 and 89 and requires 89 iterations.Can we write this statement about FastGCF's number of iterations as a mathematical formula? Since base 10 logs are proportional to the number of digits in a number (e.g. log(10) = 1, log(100) = 2, log(1000) = 3), we can define the number of digits as floor(log(N)+1) where N is the smaller number and floor truncates the decimal part (e.g., floor(10.3) = 10 and floor(10.8) = 10). Using this definition, the maximum number of iterations is 5*floor(log(N)+1). Now we can write this in big-O notation as O(5*floor(log(N)+1)). In big-O notation, we only care about the rate with respect to N. For example,
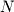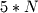and are both linear 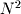and and 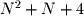are both quadratic. Because of this, O(N) and O(5*N) are considered equivalent (they both have linear complexity). With respect to FastGCF, O(5*floor(log(N)+1)) and O(log(N)) are equivalent because they both have logarithmic complexity. So, we succinctly write that the complexity of FastGCF is O(log(N)). Again, do not worry about the details of big-O notation here. It is completely unimportant to the basic programming presented in this unit. It will become extremely important in future units though when we try to compare algorithms. To develop a very basic understanding of what this means, remember that exponentials and factorials are some of the fastest growing functions and logarithms are some of the slowest growing functions in mathematics.While we discuss the importance of algorithmic efficiency at length, we should also point out that a common pitfall of novice programmers (and even experienced programmers accidentally) is to over-optimize a program. Ultimately, the fastest program is one written entirely in low-level assembly with care taken to optimize each section of code by hand. In practice, this would take eons and is simply absurd. High-level languages like Object Pascal and C++ already do their best at automatically optimizing code when they translate to assembly during compile. Of course, they cannot convert SlowGCF to FastGCF because they have no in depth knowledge about the nature of the problem of finding the greatest common factor as humans do. But as we pointed out earlier, if the purpose of the program is to compute gcfs only for small numbers or to compute a gcf only once, SlowGCF does the job just fine. If however, we are writing a mathematics library that will be used by lots of other programs, we would want to use FastGCF. The lesson here is that you should always get your code working first before worrying about optimizations. Once you know it works, then you can look for bottlenecks or parts of the code that significantly slow down the rest of the program. Loops are almost always the location of bottlenecks. But some loops are called so infrequently in a program that there is no reason to optimize them. Adopting the "good-enough" solution can save hours of programming. Parts of code that are called very frequently are called performance critical parts of code and should be optimized, but only after the program is finished. There is no reason to optimize something that does not work in the first place.
Having the fewest number of iterations is often but not always a sign of the best algorithm. If what goes on inside an iteration is very computationally complex, another algorithm with more iterations but simpler computations may be better. Again this depends on the kind of inputs you intend to feed the algorithm. This is also one of the reasons we write big-O notation as O(N) even if the actual worst case is 4*N+1 or O(log(N)) if the worst case is 5*floor(log(N)+1). We do not care about being exact in terms of the number of iterations because if one algorithm has a worst case of N and another has 4*N+1 what really matters is what happens inside the iteration and not the number of iterations. On the other hand, if one algorithm is 4*N+1 and another is 5*floor(log(N)+1), you should almost always choose the latter. To understand why, consider what happens if N = 10000. For the first one, the worst-case is 4*10000+1 = 40001. For the second, the worst case is 5*floor(log(10000)+1) = 25. It does not really matter what happens inside the iteration if one is repeated 40,001 times and the other only 25 times. Defintely pick the 25. Thus, as a general rule, algorithms that belong to the same complexity class (such as O(log N)) are pretty much equivalent unless one uses simpler operations inside the iteration. In general, the best algorithms are O(1) constant complexity, O(log N) logarithmic complexity, O(N) linear complexity, O(N^a) polynomial complexity, and O(
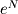) exponential complexity. Keep in mind that this is only a very small sampling of algorithm complexity. Complexity analysis is a very rich field that is well beyond the scope of this book (even the later units). Given that you have two algorithms in the same complexity class, the best one of the two will be the one that minimizes the use of floating point division (one of the most expensive operations) or large memory allocations.