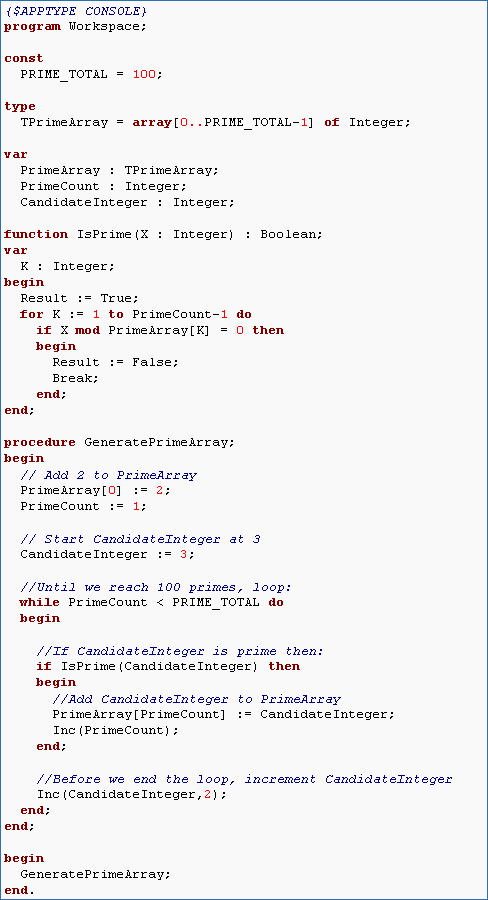
Excercise 3-12.
In this exercise we will write code to generate the first 100 primes and store them in an array. This application will be a console application. After you complete it, you will probably want to keep a copy of the code by making a copy of the folder and renaming it "Primes". Remember to use {$I Debug.inc} if you want to set breakpoints and step through the loops.
- Start with the basic template code for a console application. Declare a constant PRIME_TOTAL and set its value to 100 (we use a constant in case we want to generate more primes than the first 100 later on).
- Declare an array called TPrimeArray that has bounds 0 to PRIME_COUNT-1. Also make a variable instance of this array.
- The following pseudocode is the basic algorithm for creating an array of PRIME_TOTAL primes: Translate this pseudocode into Object Pascal code. Assume we already have a function called IsPrime that takes an integer argument and returns true if the integer is prime (we will write this function later).Set CandidateInteger to 1
Until we reach PRIME_TOTAL, loop:
If CandidateInteger is prime then:
Add CandidateInteger to PrimeArray
Output CandidateInteger to screen
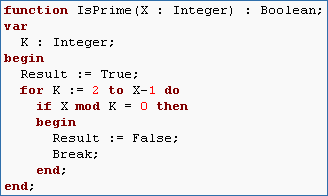
Before we end the loop, increment CandidateIntegerHint: Start by declaring the variables you will need: PrimeCount and CandidateInteger. Declare a function IsPrime that takes an integer argument but always returns True so you can debug the code (the function obviously won't find primes but we will deal with this later). This function should be declared after the variables so that it can use them later on. - The code we wrote in the previous section obviously does not return primes. We need to fill in the IsPrime function with code that correctly tests whether or not a number is prime. Don't worry about the efficiency yet. Just make a successful prime test.
Let's start with stating the mathematical rules that make an integer prime. The definition of a prime is a number that has only 2 factors: 1 and itself. So all we have to show is that a number has at least 3 factors to prove that it is not prime. A first good guess is that for a number, we could loop through all numbers less than that number and test for even divisibility. Of course, we know that the mod operator can be used to efficiently determine the remainder of an integer division. Write the IsPrime function so that it correctly tests for primeness using this method. Hint: Assume that a given integer is prime unless proven otherwise. In other words, set Result to True and then loop through all integers between 2 and X-1 looking for even divisors. If one is found, set Result to False and exit the loop immediately. - You will notice that the code in the previous problem makes one mistake. It calls 1 a prime. 0 and 1 are not primes because they have less than 2 factors. If we were worried about accuracy, we could fix this by adding an if statement to the function that excludes 0 and 1 automatically. However, since we only want to create an array of primes, we should simply start CandidateInteger at some value greater than 1 (adding an extra if statement decreases the computational efficiency of the function slightly b/c it is executed on each iteration of the loop). Speaking of computational efficiency, let's see how long our function takes to compute a large number of primes. Comment out the Writeln statement that writes primes to the screen for now. Now add the following to the beginning of the program.Writeln('Press enter to start.');
Readln;And the following at the very end.Writeln('Done.');
Readln;Set PRIME_TOTAL to around 10000 (may have to be larger or smaller depending on processor speed). When you run the program, use a stopwatch to determine the amount of time between pressing enter and the apperance of Done. If it is less than 10 seconds, increase PRIME_TOTAL until it takes more than 10 seconds to run the program (for example, try doubling it). Once we have a fairly slow program, we can consider ways of speeding it up. For example, do we need to test all integers using this method? Is there a way we can test only some integers for primeness? - In the previous problem, only modest speed increases were achieved. Are there better ways to improve the efficiency of our test? Think carefully about this one. When testing CandidateInteger for even divisibility, do we need to test every integer between 3 and CandidateInteger? If not, which ones should we test?
- Coment out the following lines in IsPrime:
 Add code that makes the loop search only through primes starting with 3 up to the largest prime determined so far. Hint: You will have to change only the lines you just commented out.
Add code that makes the loop search only through primes starting with 3 up to the largest prime determined so far. Hint: You will have to change only the lines you just commented out. - After running this program we will have an array of prime numbers. We can use this array to calculate the prime factorization of a number. First, group all of the code in the begin-end block into a procedure called GeneratePrimeArray. This is an example of modularization. We're getting the code that we know already works out of the way. We can also remove all the Writeln and Readln statements that were used for debugging.
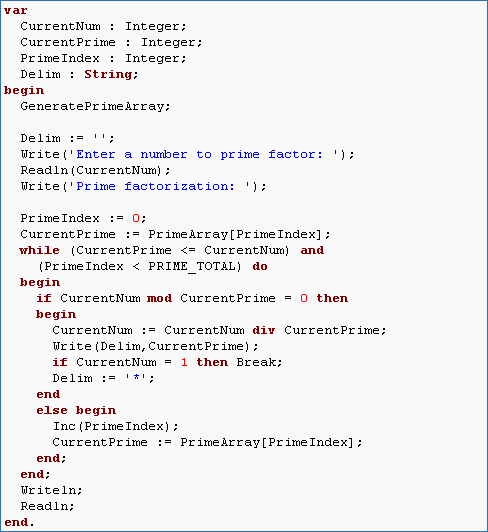
- The algorithm we will use for prime factorization is a variant of trial division. There are much faster ways of prime factoring numbers, but trial division is the simplest to understand. It is given in the following pseudocode:Store the number to factor in CurrentNum
Store the smallest prime in CurrentPrime
Repeat the following until CurrentPrime > CurrentNum:
Divide CurrentNum by CurrentPrime
If the remainder is 0 then
Store the quotient in CurrentNum
Include CurrentPrime in the factorization
otherwise move to the next primeJust to make sure you understand the algorithm, try it on some small numbers. Let's take 10. 10 divided by 2 is 5. 5 divided by 2 has a remainder so we go to the next prime. 5 divided by 3 has a remainder so we go to the next prime. 5 divided by 5 is 1. Thus, the prime factorization of 10 is 2*5. Let's try 12. 12 divided by 2 is 6. 6 divided by 2 is 3. 3 divided by 2 has a remainder so we go to the next prime. 3 divided by 3 is 1 so the prime factorization of 12 is 2*2*3. Translate this pseudocode into actual code. By "Include CurrentPrime in the factorization" you can simply write the prime factors to the screen.





 . 15 can be written as
. 15 can be written as 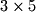 . Given these prime factorizations we know that if a number is divisible by 9 then it must be divisible by 3. If a number is divisible by 15 then it must be divisible by both 3 and 5. So there is no reason to test for divisibility with non-prime numbers. While this doesn't matter for many numbers, consider numbers such as 1517. The prime factorization of 1517 is
. Given these prime factorizations we know that if a number is divisible by 9 then it must be divisible by 3. If a number is divisible by 15 then it must be divisible by both 3 and 5. So there is no reason to test for divisibility with non-prime numbers. While this doesn't matter for many numbers, consider numbers such as 1517. The prime factorization of 1517 is 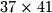 . Since 37 and 41 are both primes, testing 1517 for divisibility by 3, 4, 5, 6, 7, etc is a waste of time. We could simply use the primes in PrimeArray to test for divisibility. In other words we would have eleven numbers to check: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37. This saves (37-3+1)-(11) = 24 iterations of the loop. As our numbers become larger, these savings will become larger as well.
. Since 37 and 41 are both primes, testing 1517 for divisibility by 3, 4, 5, 6, 7, etc is a waste of time. We could simply use the primes in PrimeArray to test for divisibility. In other words we would have eleven numbers to check: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37. This saves (37-3+1)-(11) = 24 iterations of the loop. As our numbers become larger, these savings will become larger as well.