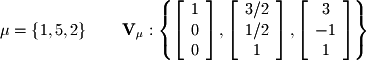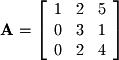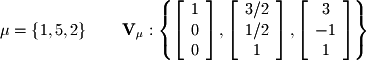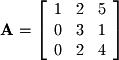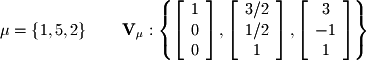freetext.org
Home
Back to Chapter Contents
Prev
|
Next Section
Excercise 8-2.
Diagonalize the following matrix
given the following:
To find the matrix diagonalization we need to know
,
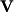
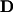
, and
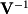
. The first two of these matrices are simply the eigenvectors and eigenvalues:
We can now find
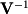
through row reduction of [
|
]:
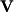
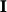
With these matrices, the diagonalization of A is given by the following:
Show Solution
Back to Chapter Contents
Prev
|
Next Section
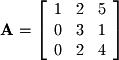given the following:
, 
, and 
. The first two of these matrices are simply the eigenvectors and eigenvalues:
through row reduction of [
|
]: 
