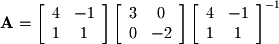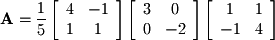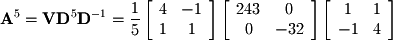Diagonalized matrices take the form 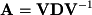 where the matrix
where the matrix 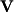 represents a set of eigenvectors (a basis for eigenspace) and
represents a set of eigenvectors (a basis for eigenspace) and 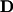 is a diagonal matrix (zeros everywhere but the diagonal) containing the eigenvalues. For example, given that
is a diagonal matrix (zeros everywhere but the diagonal) containing the eigenvalues. For example, given that 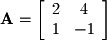 and
and 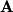 has eigenvalues
has eigenvalues 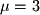 and
and 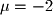 with eigenvectors
with eigenvectors 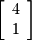 and
and 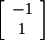 respectively, we find the following diagonalization for
respectively, we find the following diagonalization for 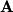 :
: 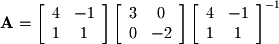
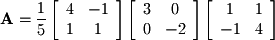 Diagonalizaed matrices are useful for many things such as raising a matrix to a power:
Diagonalizaed matrices are useful for many things such as raising a matrix to a power: 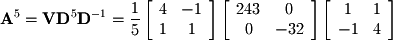

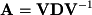 where the matrix
where the matrix 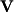 represents a set of eigenvectors (a basis for eigenspace) and
represents a set of eigenvectors (a basis for eigenspace) and 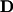 is a diagonal matrix (zeros everywhere but the diagonal) containing the eigenvalues. For example, given that
is a diagonal matrix (zeros everywhere but the diagonal) containing the eigenvalues. For example, given that 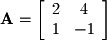 and
and 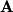 has eigenvalues
has eigenvalues 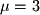 and
and 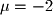 with eigenvectors
with eigenvectors 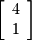 and
and 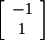 respectively, we find the following diagonalization for
respectively, we find the following diagonalization for 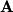 :
: