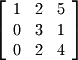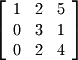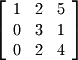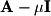
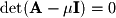
The matrix is given by the following:   We can find the determinant of this matrix by expanding down the first column (because it has the most zeros):  The eigenvalues are the solution to or . Given these eigenvalues, we need to find eigenvectors for each of them.

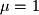
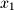
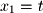
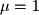
For :   Since there is no pivot for , we set :   The eigenvector for is .

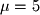
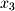
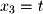
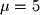
For :  There is no pivot for here so we set :   The eigenvector for is .

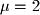
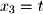
For :   Again, there is no pivot for here so we set :   The eigenvector for is .