The answer is none of them. A common mistake that students make is to cross two of the points in the plane in order to determine the normal. You CANNOT cross points! Using the coordinates of these points in the cross product formula amounts to crossing the vectors to these points. It is very important to realize the difference between vectors in a plane and points in a plane. Figures
4-2 and
4-3 show the difference. In Figure
4-3, note that the vectors to the points in a plane lie outside the plane. This is the reason the cross product would fail.
Say you actually chose
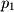
and
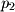
and crossed the vectors

and
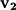
to these points:
This would give the vector perpendicular to
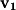
and
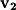
, but not to the plane containing all three points. Drawing a plane with this normal clearly shows the error:
What we need are two vectors that actually lie in the plane in order to cross them and get the appropriate normal.
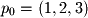 ,
, 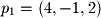 , and
, and 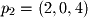 , which points need to be crossed in order to find the normal to the plane?
, which points need to be crossed in order to find the normal to the plane? 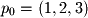 ,
, 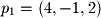 , and
, and 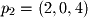 , which points need to be crossed in order to find the normal to the plane?
, which points need to be crossed in order to find the normal to the plane? 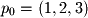 ,
, 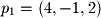 , and
, and 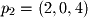 , which points need to be crossed in order to find the normal to the plane?
, which points need to be crossed in order to find the normal to the plane?