Excercise 4-2.
Given the same three points from the last exercise (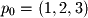 ,
, 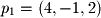 , and
, and 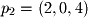 ), determine two vectors in the plane and cross these vectors to find the standard equation for a plane.
), determine two vectors in the plane and cross these vectors to find the standard equation for a plane.
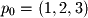 ,
, 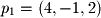 , and
, and 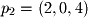 ), determine two vectors in the plane and cross these vectors to find the standard equation for a plane.
), determine two vectors in the plane and cross these vectors to find the standard equation for a plane. 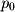 and
and 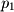 as shown below, by vector subtraction we know that
as shown below, by vector subtraction we know that 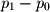 is a vector with its head at
is a vector with its head at 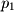 and tail at
and tail at 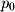 .
.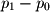 and
and 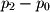 to cross, but the same result is obtained if one crosses
to cross, but the same result is obtained if one crosses 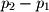 with either of these vectors as well.
with either of these vectors as well.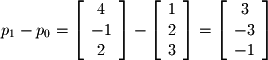
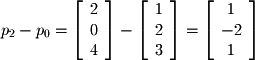
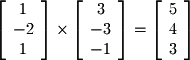
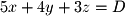 .
. 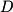 is found by plugging in any of the given points in a plane.
is found by plugging in any of the given points in a plane.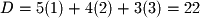
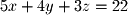 .
.