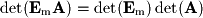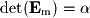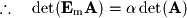Row operations have very well-defined effects on the determinant of a matrix and this can be most easily seen with elementary matrices. First remember the rule for the determinant of a matrix product: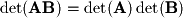
We will demonstrate the effect on the determinant for a system with 3 equations, but these rules hold for any number of 
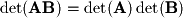
equations.
equations. - Starting with interchanging two rows:
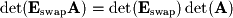
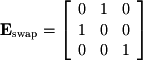
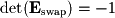
- Next, multiplying by one row and adding to another:
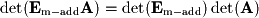
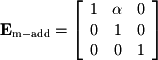
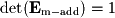
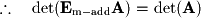
- Finally, multiplying by a row by a nonzero scalar:
