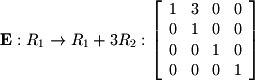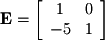Given that a matrix inverse keeps a record of the cumulative row operations performed to bring a matrix to RREF, it is also sometimes useful to represent a single row operation as an elementary matrix. An elementary matrix for a single row operation can be found by performing that operation on the 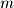 -by-
-by-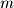 identity matrix where
identity matrix where 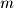 is the number of equations in the system. For example
is the number of equations in the system. For example 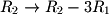 is represented by the following matrix:
is represented by the following matrix: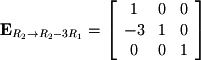 Once again, the row operations for the matrix used in previous subsections will be used to demonstrate elementary matrices:
Once again, the row operations for the matrix used in previous subsections will be used to demonstrate elementary matrices: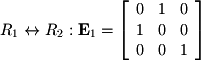
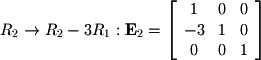
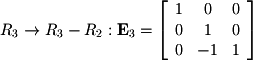
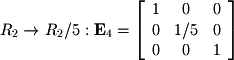
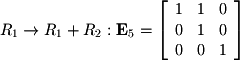 Multiplying all of these matrices together at once gives the matrix inverse. Note the order of multiplication. The order of row operations corresponds to a right-to-left order in multiplication:
Multiplying all of these matrices together at once gives the matrix inverse. Note the order of multiplication. The order of row operations corresponds to a right-to-left order in multiplication: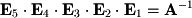
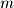 -by-
-by-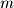 identity matrix where
identity matrix where 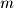 is the number of equations in the system. For example
is the number of equations in the system. For example 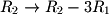 is represented by the following matrix:
is represented by the following matrix: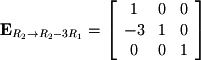
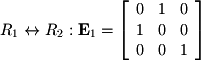
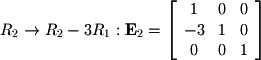
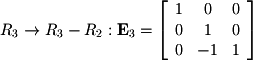
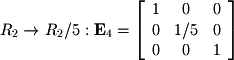
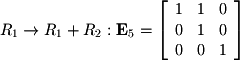
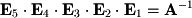
Excercise 5-6.
Write the following elementary matrices:
- The row operation
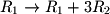 for a system with
for a system with 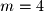 equations and
equations and 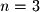 unknowns.
unknowns. - The row operation
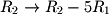 for a system with
for a system with 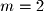 equations and
equations and 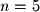 unknowns.
unknowns.
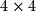 elementary matrix is found by the following:
elementary matrix is found by the following: