Finally, it is helpful to understand what all of the terms in the general equation mean. If you think back to the equation of a line (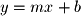 ) in 2-dimensions you will remember that all the lines with the same slope are parallel. The equation
) in 2-dimensions you will remember that all the lines with the same slope are parallel. The equation 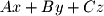 has a similar property. All planes with equations that have the same
has a similar property. All planes with equations that have the same 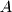 ,
, 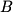 , and
, and 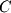 (or scalar multiples of these constants) will be parallel.
(or scalar multiples of these constants) will be parallel.
Also, just as the "b" in the equation of a line represents the intercept of a line with the y-axis, the "D" in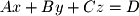 represents the plane's distance from the origin along its unit normal. Figure 4-6 below illustrates these properties graphically.
represents the plane's distance from the origin along its unit normal. Figure 4-6 below illustrates these properties graphically.
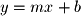 ) in 2-dimensions you will remember that all the lines with the same slope are parallel. The equation
) in 2-dimensions you will remember that all the lines with the same slope are parallel. The equation 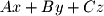 has a similar property. All planes with equations that have the same
has a similar property. All planes with equations that have the same 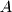 ,
, 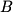 , and
, and 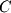 (or scalar multiples of these constants) will be parallel.
(or scalar multiples of these constants) will be parallel.Also, just as the "b" in the equation of a line represents the intercept of a line with the y-axis, the "D" in
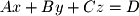 represents the plane's distance from the origin along its unit normal. Figure 4-6 below illustrates these properties graphically.
represents the plane's distance from the origin along its unit normal. Figure 4-6 below illustrates these properties graphically.Object could not be loaded.
Figure 4-6. Definition of a Plane by Standard Equation Coefficients